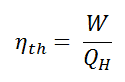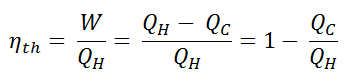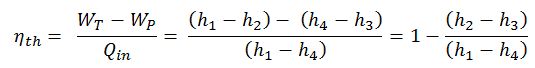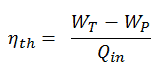Theory of Rankine Cycle
The Rankine cycle was named after him and describes the performance of steam turbine systems, though the theoretical principle also applies to reciprocating engines such as steam locomotives. The Rankine cycle is an idealized thermodynamic cycle of a constant pressure heat engine that converts part of heat into mechanical work. In this cycle, the heat is supplied externally to a closed loop, which usually uses water (in a liquid and vapor phase) as the working fluid. In contrast to the Brayton cycle, the working fluid in the Rankine cycle undergo the phase change from a liquid to vapor phase and vice versa.
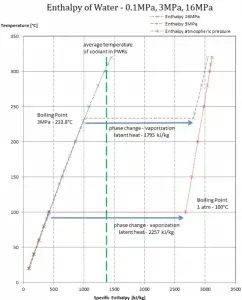
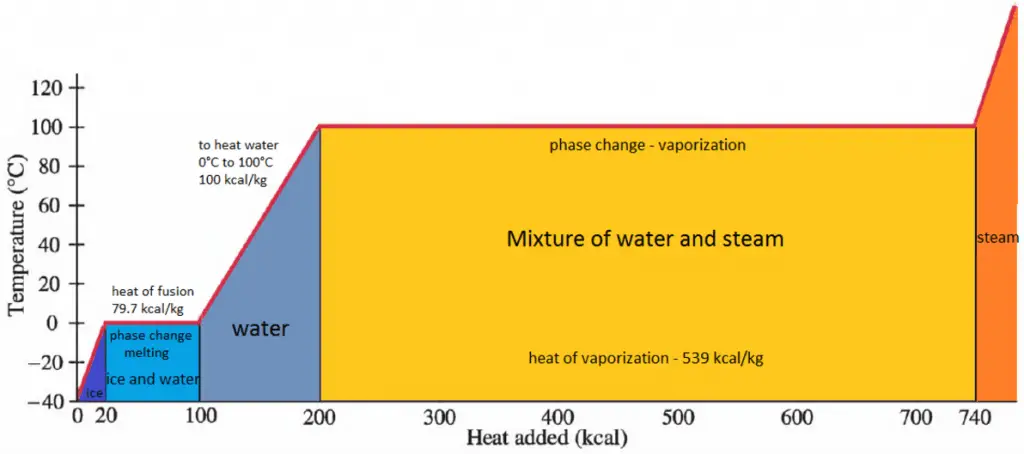
While many substances could be used as the working fluid in the Rankine cycle (inorganic or even organic), water is usually the fluid of choice due to its favorable properties, such as its non-toxic and unreactive chemistry, abundance, and low cost, as well as its thermodynamic properties. For example, water has the highest specific heat of any common substance – 4.19 kJ/kg K. Moreover it has a very high heat of vaporization, making it an effective coolant and medium in thermal power plants and other energy industries. In the case of the Rankine cycle, the Ideal Gas Law almost cannot be used (steam does not follow pV=nRT). Therefore all important parameters of water and steam are tabulated in so-called “Steam Tables”.
One of the major advantages of the Rankine cycle is that the compression process in the pump takes place on a liquid. By condensing the working steam to a liquid (inside a condenser), the pressure at the turbine outlet is lowered, and the energy required by the feed pump consumes only 1% to 3% of the turbine output power. These factors contribute to higher efficiency for the cycle.
In an ideal Rankine cycle, the system executing the cycle undergoes a series of four processes: two isentropic (reversible adiabatic) processes alternated with two isobaric processes:
-
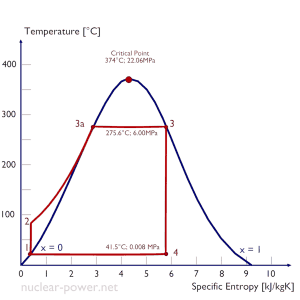
Rankine Cycle – Ts Diagram Isentropic compression (compression in centrifugal pumps) – The liquid condensate is compressed adiabatically from state 1 to state 2 by centrifugal pumps (usually by condensate pumps and then by feedwater pumps). The liquid condensate is pumped from the condenser into the higher pressure boiler. In this process, the surroundings work on the fluid, increasing its enthalpy (h = u+pv) and compressing it (increasing its pressure). On the other hand, the entropy remains unchanged. The work required for the compressor is given by WPumps = H2 – H1.
- Isobaric heat addition (in a heat exchanger – boiler) – In this phase (between state 2 and state 3), there is a constant-pressure heat transfer to the liquid condensate from an external source since the chamber is open to flow in and out. The feedwater (secondary circuit) is heated to the boiling point (2 → 3a) of that fluid and then evaporated in the boiler (3a → 3). The net heat added is given by Qadd = H3 – H2
- Isentropic expansion (expansion in a steam turbine) – Steam from the boiler expands adiabatically from state 3 to state 4 in a steam turbine to produce work and then is discharged to the condenser (partially condensed). The steam works on the surroundings (blades of the turbine) and loses an amount of enthalpy equal to the work that leaves the system. The work done by the turbine is given by WT = H4 – H3. Again the entropy remains unchanged.
- Isobaric heat rejection (in a heat exchanger) – In this phase, the cycle completes by a constant-pressure process in which heat is rejected from the partially condensed steam. There is heat transfer from the vapor to cooling water flowing in a cooling circuit. The vapor condenses, and the temperature of the cooling water increases. The net heat rejected is given by Qre = H4 – H1
During a Rankine cycle, the pumps’ work is done on the fluid between states 1 and 2 (isentropic compression). Work is done by the fluid in the turbine between stages 3 and 4 (isentropic expansion). The difference between the work done by the fluid and the work done on the fluid is the network produced by the cycle, and it corresponds to the area enclosed by the cycle curve (in the pV diagram). The working fluid in a Rankine cycle follows a closed loop and is reused constantly.
As can be seen, it is convenient to use enthalpy and the first law in terms of enthalpy to analyze this thermodynamic cycle. This form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:
Isobaric process (Vdp = 0):
dH = dQ → Q = H2 – H1
At constant entropy, i.e., in isentropic process, the enthalpy change equals the flow process work done on or by the system:
Isentropic process (dQ = 0):
dH = Vdp → W = H2 – H1
See also: Why power engineers use enthalpy? Answer: dH = dQ + Vdp
Isentropic Process
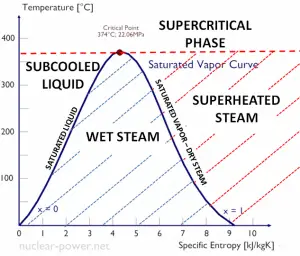
An isentropic process is a thermodynamic process in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. The assumption of no heat transfer is very important since we can use the adiabatic approximation only in very rapid processes.
Isentropic Process and the First Law
For a closed system, we can write the first law of thermodynamics in terms of enthalpy:
dH = dQ + Vdp
or
dH = TdS + Vdp
Isentropic process (dQ = 0):
dH = Vdp → W = H2 – H1
Isobaric Process
An isobaric process is a thermodynamic process in which the system’s pressure remains constant (p = const). The heat transfer into or out of the system does work and changes the system’s internal energy.
Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as:
H = U + pV
Isobaric Process and the First Law
The classical form of the first law of thermodynamics is the following equation:
dU = dQ – dW
In this equation, dW is equal to dW = pdV and is known as the boundary work. In an isobaric process and the ideal gas, part of the heat added to the system will be used to do work, and part of the heat added will increase the internal energy (increase the temperature). Therefore it is convenient to use enthalpy instead of internal energy.
Isobaric process (Vdp = 0):
dH = dQ → Q = H2– H1
At constant entropy, i.e., in isentropic process, the enthalpy change equals the flow process work done on or by the system.
Thermal Efficiency of Rankine Cycle
In general, the thermal efficiency, ηth, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, QH.
The thermal efficiency, ηth, represents the fraction of heat, QH, converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:
This is a very useful formula, but we express the thermal efficiency using the first law in terms of enthalpy.
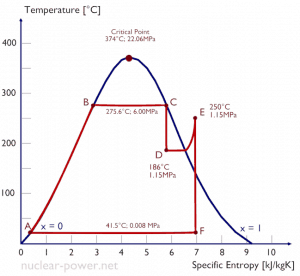
Typically most nuclear power plants operate multi-stage condensing steam turbines. In these turbines, the high-pressure stage receives steam (this steam is nearly saturated steam – x = 0.995 – point C at the figure; 6 MPa; 275.6°C) from a steam generator and exhausts it to moisture separator-reheater (point D). The steam must be reheated to avoid damages caused to the steam turbine blades by low-quality steam. The reheater heats the steam (point D), and then the steam is directed to the low-pressure stage of the steam turbine, where it expands (point E to F). The exhausted steam then condenses in the condenser. It is at a pressure well below atmospheric (absolute pressure of 0.008 MPa) and is in a partially condensed state (point F), typically of a quality near 90%.
In this case, steam generators, steam turbines, condensers, and feedwater pumps constitute a heat engine subject to the efficiency limitations imposed by the second law of thermodynamics. In an ideal case (no friction, reversible processes, perfect design), this heat engine would have a Carnot efficiency of
= 1 – Tcold/Thot = 1 – 315/549 = 42.6%
where the temperature of the hot reservoir is 275.6°C (548.7K), the temperature of the cold reservoir is 41.5°C (314.7K). But the nuclear power plant is the real heat engine, in which thermodynamic processes are somehow irreversible. They are not done infinitely slowly. In real devices (turbines, pumps, and compressors), mechanical friction and heat losses cause further efficiency losses.
To calculate the thermal efficiency of the simplest Rankine cycle (without reheating), engineers use the first law of thermodynamics in terms of enthalpy rather than in terms of internal energy.
The first law in terms of enthalpy is:
dH = dQ + Vdp
In this equation, the term Vdp is a flow process work. This work, Vdp, is used for open flow systems like a turbine or a pump in which there is a “dp,” i.e., change in pressure. There are no changes in the control volume. As can be seen, this form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:
Isobaric process (Vdp = 0):
dH = dQ → Q = H2 – H1
At constant entropy, i.e., in isentropic process, the enthalpy change equals the flow process work done on or by the system:
Isentropic process (dQ = 0):
dH = Vdp → W = H2 – H1
It is obvious, and it will be very useful in the analysis of both thermodynamic cycles used in power engineering, i.e., in the Brayton and Rankine cycles.
The enthalpy can be made into an intensive or specific variable by dividing by the mass. Engineers use the specific enthalpy in thermodynamic analysis more than the enthalpy itself. It is tabulated in the steam tables along with specific volume and specific internal energy. The thermal efficiency of such a simple Rankine cycle and in terms of specific enthalpies would be:
It is a very simple equation, and for the determination of the thermal efficiency, you can use data from steam tables.
In modern nuclear power plants, the overall thermal efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power. The reason lies in relatively low steam temperature (6 MPa; 275.6°C). Higher efficiencies can be attained by increasing the temperature of the steam. But this requires an increase in pressures inside boilers or steam generators. However, metallurgical considerations place upper limits on such pressures. In comparison to other energy sources, the thermal efficiency of 33% is not much. But it must be noted that nuclear power plants are much more complex than fossil fuel power plants, and it is much easier to burn fossil fuel than to generate energy from nuclear fuel. Sub-critical fossil fuel power plants operated under critical pressure (i.e., lower than 22.1 MPa) can achieve 36–40% efficiency.
Rankine Cycle – Equations and Calculation
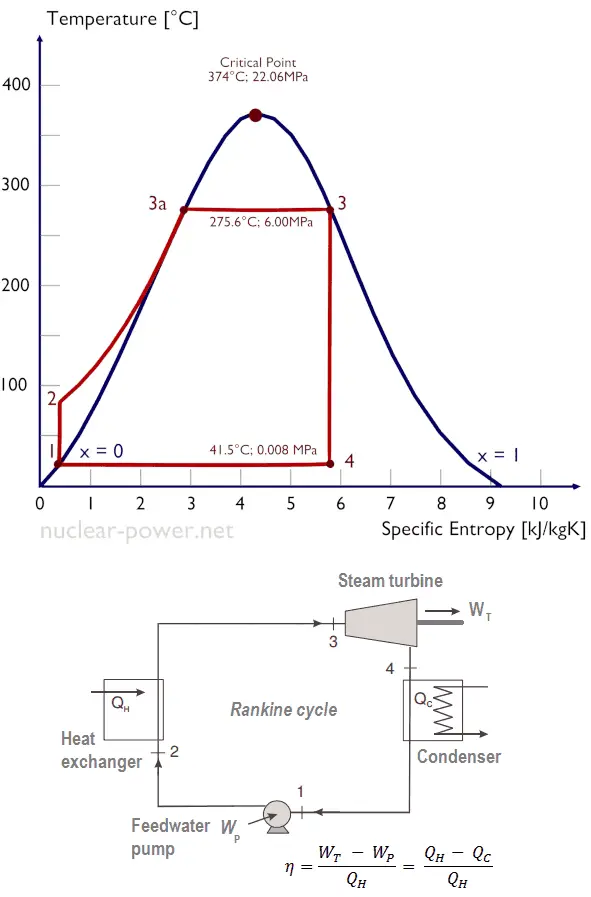 Let us assume the Rankine cycle, one of the most common thermodynamic cycles in thermal power plants. In this case, assume a simple cycle without reheat and without condensing steam turbine running on saturated steam (dry steam). In this case, the turbine operates at a steady state with inlet conditions of 6 MPa, t = 275.6°C, x = 1 (point 3). Steam leaves this turbine stage at a pressure of 0.008 MPa, 41.5°C, and x = ??? (point 4).
Let us assume the Rankine cycle, one of the most common thermodynamic cycles in thermal power plants. In this case, assume a simple cycle without reheat and without condensing steam turbine running on saturated steam (dry steam). In this case, the turbine operates at a steady state with inlet conditions of 6 MPa, t = 275.6°C, x = 1 (point 3). Steam leaves this turbine stage at a pressure of 0.008 MPa, 41.5°C, and x = ??? (point 4).
Calculate:
- The vapor quality of the outlet steam.
- The enthalpy difference between these two states (3 → 4) corresponds to the work done by the steam, WT.
- The enthalpy difference between these two states (1 → 2) corresponds to the work done by pumps, WP.
- The enthalpy difference between these two states (2 → 3) corresponds to the steam generator’s net heat.
- The thermodynamic efficiency of this cycle and compare this value with Carnot’s efficiency.
1)
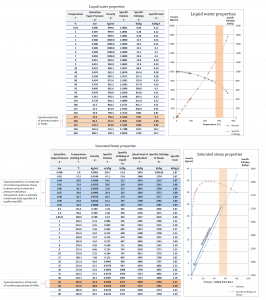
Since we do not know the exact vapor quality of the outlet steam, we have to determine this parameter. State 4 is fixed by the pressure p4 = 0.008 MPa and the fact that the specific entropy is constant for the isentropic expansion (s3 = s4 = 5.89 kJ/kgK for 6 MPa). The specific entropy of saturated liquid water (x=0) and dry steam (x=1) can be picked from steam tables. In the case of wet steam, the actual entropy can be calculated with the vapor quality, x, and the specific entropies of saturated liquid water and dry steam:
s4 = sv x + (1 – x ) sl
where
s4 = entropy of wet steam (J/kg K) = 5.89 kJ/kgK
sv = entropy of “dry” steam (J/kg K) = 8.227 kJ/kgK (for 0.008 MPa)
sl = entropy of saturated liquid water (J/kg K) = 0.592 kJ/kgK (for 0.008 MPa)
From this equation the vapor quality is:
x4 = (s4 – sl) / (sv – sl) = (5.89 – 0.592) / (8.227 – 0.592) = 0.694 = 69.4%
2)
The enthalpy for the state 3 can be picked directly from steam tables, whereas the enthalpy for the state 4 must be calculated using vapor quality:
h3, v = 2785 kJ/kg
h4, wet = h4,v x + (1 – x ) h4,l = 2576 . 0.694 + (1 – 0.694) . 174 = 1787 + 53.2 = 1840 kJ/kg
Then the work done by the steam, WT, is
WT = Δh = 945 kJ/kg
3)
Enthalpy for state 1 can be picked directly from steam tables:
h1, l = 174 kJ/kg
State 2 is fixed by the pressure p2 = 6.0 MPa and the fact that the specific entropy is constant for the isentropic compression (s1 = s2 = 0.592 kJ/kgK for 0.008 MPa). For this entropy s2 = 0.592 kJ/kgK and p2 = 6.0 MPa we find h2, subcooled in steam tables for compressed water (using interpolation between two states).
h2, subcooled = 179.7 kJ/kg
Then the work done by the pumps, WP, is
WP = Δh = 5.7 kJ/kg
4)
The enthalpy difference between (2 → 3), which corresponds to the net heat added in the steam generator, is simply:
Qadd = h3, v – h2, subcooled = 2785 – 179.7 = 2605.3 kJ/kg
Note that there is no heat regeneration in this cycle. On the other hand, most of the heat added is for the enthalpy of vaporization (i.e., for the phase change).
5)
In this case, steam generators, steam turbines, condensers, and feedwater pumps constitute a heat engine subject to the efficiency limitations imposed by the second law of thermodynamics. In the ideal case (no friction, reversible processes, perfect design), this heat engine would have a Carnot efficiency of
ηCarnot = 1 – Tcold/Thot = 1 – 315/549 = 42.6%
where the temperature of the hot reservoir is 275.6°C (548.7 K), the temperature of the cold reservoir is 41.5°C (314.7K).
The thermodynamic efficiency of this cycle can be calculated by the following formula:
thus
ηth = (945 – 5.7) / 2605.3 = 0.361 = 36.1%