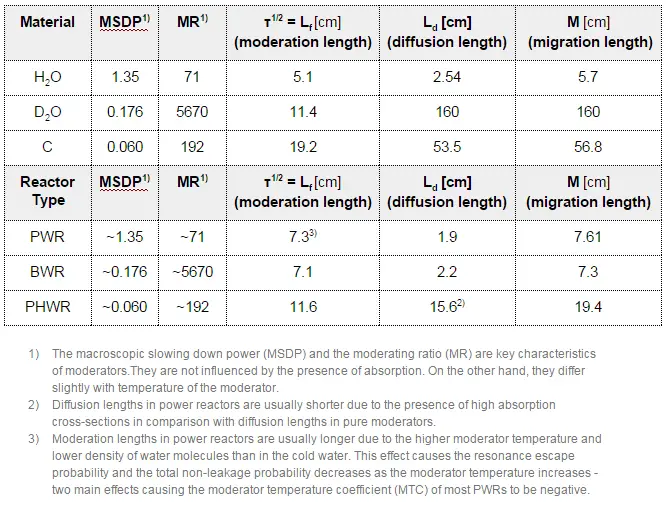
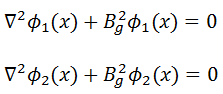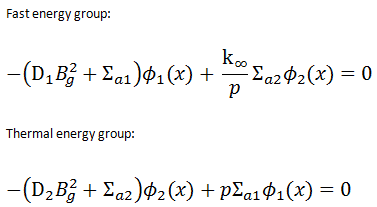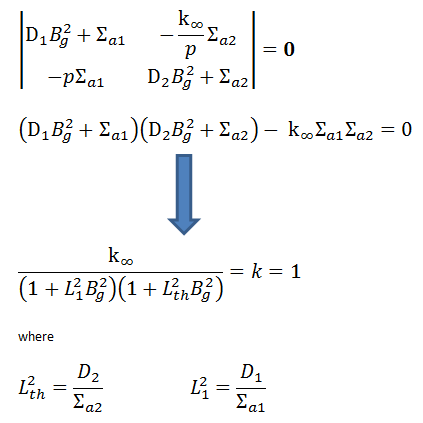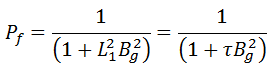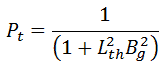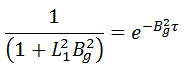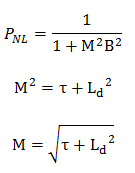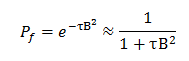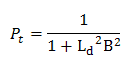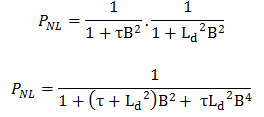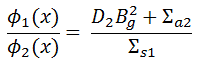We have used a very important assumption in previous sections that all neutrons are lumped into a single energy group. These monoenergetic neutrons are emitted and diffuse at thermal energy (0.025 eV). In a thermal reactor, the neutrons have distribution in the energy. The spectrum of neutron energies produced by fission varies significantly with certain reactor designs. The figure illustrates the difference in neutron flux spectra between a thermal reactor and a fast breeder reactor. Note that the neutron spectra in fast reactors also vary significantly with a given reactor coolant.
See also: Neutron Flux Spectra.
In general, free neutrons can be divided into many energy groups. The reactor physics does not need a fine division of neutron energies. The neutrons can be roughly (for purposes of reactor physics) divided into three energy ranges:
- Thermal neutrons (0.025 eV – 1 eV)
- Resonance neutrons (1 eV – 1 keV)
- Fast neutrons (1 keV – 10 MeV)
Even there are reactor computing codes that use only two neutron energy groups:
- Slow neutrons group (0.025 eV – 1 keV).
- Fast neutrons group (1 keV – 10 MeV).
- Cold Neutrons (0 eV; 0.025 eV). Neutrons in thermal equilibrium with very cold surroundings such as liquid deuterium. This spectrum is used for neutron scattering experiments.
- Thermal Neutrons. Neutrons in thermal equilibrium with a surrounding medium. Most probable energy at 20°C (68°F) for Maxwellian distribution is 0.025 eV (~2 km/s). This part of the neutron’s energy spectrum constitutes the most important spectrum in thermal reactors.
- Epithermal Neutrons (0.025 eV; 0.4 eV). Neutrons of kinetic energy are greater than thermal. Some reactor designs operate with an epithermal neutron spectrum. This design allows reaching a higher fuel breeding ratio than in thermal reactors.
-
Neutrons of kinetic energy below the cadmium cut-off energy (~0.5 eV) are strongly absorbed by 113-Cd.
Source: JANIS (Java-based nuclear information software) www.oecd-nea.org/janis/Cadmium Neutrons (0.4 eV; 0.5 eV). Neutrons of kinetic energy below the cadmium cut-off energy. One cadmium isotope, 113Cd, absorbs neutrons strongly only if they are below ~0.5 eV (cadmium cut-off energy).
- Epicadmium Neutrons (0.5 eV; 1 eV). Neutrons of kinetic energy above the cadmium cut-off energy. These neutrons are not absorbed by cadmium.
- Slow Neutrons (1 eV; 10 eV).
- Resonance Neutrons (10 eV; 300 eV). The resonance neutrons are called resonance for their special behavior. At resonance energies, the cross-sections can reach peaks more than 100x higher than the base value of the cross-section. At these energies, the neutron capture significantly exceeds the probability of fission. Therefore it is very important (for thermal reactors) to quickly overcome this range of energy and operate the reactor with thermal neutrons results in increasing the probability of fission.
- Intermediate Neutrons (300 eV; 1 MeV).
- Fast Neutrons (1 MeV; 20 MeV). Neutrons of kinetic energy greater than 1 MeV (~15 000 km/s) are usually named fission neutrons. These neutrons are produced by nuclear processes such as nuclear fission or (ɑ,n) reactions. The fission neutrons mean energy (for 235U fission) of 2 MeV. Inside a nuclear reactor, the fast neutrons are slowed down to thermal energies via neutron moderation.
- Relativistic Neutrons (20 MeV; ->)
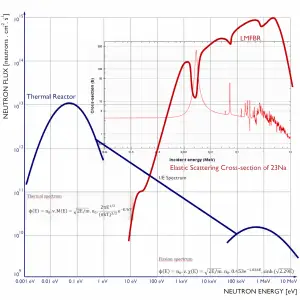
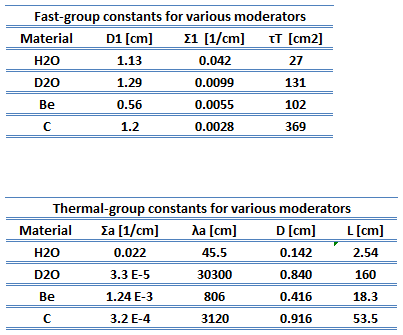One of the most effective ways of calculating the neutron diffusion in thermal reactors is by the multigroup diffusion method. In this method, the entire range of neutron energies is divided into N intervals. All neutrons within each interval are lumped into a group, and in this group, all parameters such as the diffusion coefficients or cross-sections are averaged.
As an illustrative example, we will show a two-group diffusion equation and briefly demonstrate its solution. In this example, we consider a thermal energy group and combine all neutrons of a higher energy into a fast energy group.
In steady-state, the diffusion equations for the fast and thermal energy groups are:
The equations are coupled through the thermal fission term the fast removal term. In this system of equations, we assume that neutrons appear in the fast group due to fission induced by thermal neutrons (therefore Φ2(x)). In the fission term, k∞ is to infinite multiplication factor, and p is the resonance escape probability. The fast absorption term expresses neutrons that are lost from the fast group by slowing down. Σa1Φ1 is equal to the thermal slowing down density.
Consider the second equation (thermal energy group). Neutrons enter the thermal group as a result of slowing down out of the fast group. Therefore the term pΣa1Φ1 in this equation comes from the fast group. It represents the source of neutrons that escaped to resonance absorption.
To solve this system of equations we assume for a uniform reactor, that both groups of the fluxes in the core have a geometrical buckling Bg satisfying:
Since the geometrical buckling is the same for both the thermal and fast fluxes, the diffusion equations can be rewritten as:
Criticality Equation for Two-group Theory and Bare Reactor
The solution of this pair of homogeneous algebraic equations leads to a determinant of the coefficients, which have the following solution (using Cramer’s rule):
The previous equation is usually referred to as the criticality equation. In this equation, the terms
is known as the fast non-leakage factor and
is known as the thermal non-leakage factor.
For weakly absorbing media and according to Fermi Theory, the following relation can be aplied:
- The source distribution, whether it is an external source of neutrons or is a multiplying environment.
- The geometry (in a finite medium).
- The neutron diffusion length, L2 = D/Σa L2, is the diffusion area. It is proportional to the distance thermal neutrons travel before they are absorbed.
- The slowing-down length, Ls, of a neutron. It is proportional to the distance fast neutrons travel from when they are born to the point where they become thermalized. Since it can be derived from Fermi age theory, a parameter τ, called the “age” (often called the “Fermi age”), is often used.
Let us focus on the diffusion length and the slowing-down length.
The physical meaning of the diffusion length is that:
L2 is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a thermal neutron) and its absorption.
The Fermi age is related to the distance traveled during moderation, just as the diffusion length is for thermal neutrons. The Fermi age is the same quantity as the slowing-down length squared, Ls2, but the slowing-down length is the square root of the Fermi age, τth = Ls2. The physical meaning of the slowing-down length is:
Ls2 is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a fast neutron) and the point where it has become thermalized.
Let us define the quantity, M2, where:
M2 = L2 + Ls2 or M2 = L2 + τth
This quantity is called the migration area or square of the migration length. The physical meaning of the migration area is:
M2 is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a fast neutron) and its absorption (as a thermal neutron).
The distance traveled by fast neutrons during moderation and the distance traveled by thermal neutrons during diffusion in a reactor is important to reactor design because of their effect on the critical size and their effect on the neutron leakage.
Effect on the Neutron Leakage
It can be derived the total non-leakage probability of large reactors is primarily a function of migration area.
Fast Non-leakage Probability
It can be derived from the Fermi age theory, the probability that a neutron will remain in the core and become a thermal neutron without being lost by fast leakage is also represented by the following equation:
where τ is the Fermi age of the neutron, B is the geometrical buckling (in case of critical state Bg = Bm), which depends only on the shape and size of the core. The value of B for small cores is higher than the value for large cores. So that, it is obvious, the fast neutrons leakage is higher for small cores and depends on the macroscopic slowing down the power of neutron moderator (leakage is higher for poor moderators).
Thermal Non-leakage Probability
It can be derived from the neutron diffusion theory. The probability that a thermal neutron will remain in the core is also represented by the following equation:
in which Ld is the diffusion length, B is the geometrical buckling (in case of critical state Bg = Bm), which depends only on the shape and size of the core. The value of B for small cores is higher than the value for large cores.
Total Non-leakage Probability
The fast non-leakage probability (Pf) and the thermal non-leakage probability (Pt) may be combined into one term that gives the fraction of all neutrons that do not leak out of the reactor core. This term is called the total non-leakage probability and is given the symbol PNL, and may be expressed by the following equation:
We can rewrite this equation without a substantial loss of accuracy for large reactors simply by replacing the diffusion length Ld and the fermi age τ with the migration length M in the one group equation. The term B4 is very small for large reactors, and therefore it can be neglected. We may then write.
where M is the migration area (m2), the migration length is defined as the square root of the migration area. As can be seen, the total non-leakage probability of large reactors is primarily a function of the migration area.
Flux Distribution for Two-group Theory and Bare Reactor
For a uniform reactor, the vanishing of the neutron flux on the boundary requires that the neutron flux in both groups satisfies:
Since the geometrical buckling is the same for both the thermal and fast fluxes, the thermal flux and the fast-flux are proportional to the bare reactor. It can be derived that:
