As in the Carnot, Otto, and Brayton cycle, the thermal efficiency tends to increase as the average temperature at which energy is added by heat transfer increases and/or the average temperature at which energy is rejected decreases. This is the common feature of all thermodynamic cycles.
Condenser Pressure
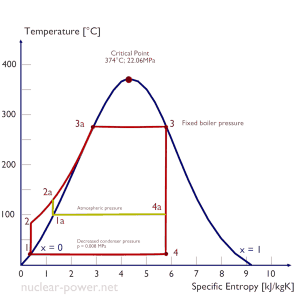
The case of the decrease in the average temperature at which energy is rejected requires a decrease in the pressure inside the condenser (i.e., the decrease in the saturation temperature). The lowest feasible condenser pressure is the saturation pressure corresponding to the ambient temperature (i.e., the absolute pressure of 0.008 MPa, which corresponds to 41.5°C). The goal of maintaining the lowest practical turbine exhaust pressure is a primary reason for including the condenser in a thermal power plant. The condenser provides a vacuum that maximizes the energy extracted from the steam, resulting in a significant increase in network and thermal efficiency. But also this parameter (condenser pressure) has its engineering limits:
- Decreasing the turbine exhaust pressure decreases the vapor quality (or dryness fraction). At some point, the expansion must be ended to avoid damages caused to steam turbine blades by low-quality steam.
- Decreasing the turbine exhaust pressure significantly increases the specific volume of exhausted steam, which requires huge blades in the last rows of the low-pressure stage of the steam turbine.
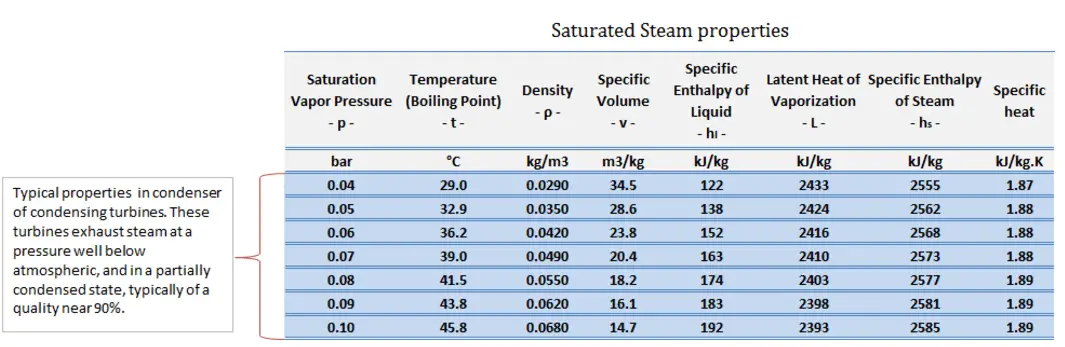
In typical wet steam turbines, the exhausted steam condenses in the condenser, and it is at a pressure well below atmospheric (absolute pressure of 0.008 MPa, which corresponds to 41.5°C). This steam is in a partially condensed state (point F), typically of a quality near 90%. Note that there is always a temperature difference between (around ΔT = 14°C) the condenser temperature and the ambient temperature, which originates from condensers’ finite size and efficiency.
Boiler Pressure
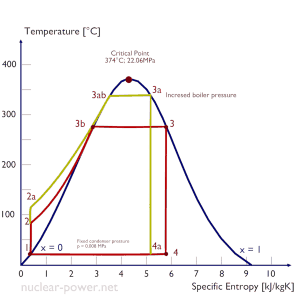
The increase in the average temperature at which energy is added by heat transfer requires either superheating of steam produced or an increase in the pressure in the boiler (steam generator). Superheating is not typical for nuclear power plants.
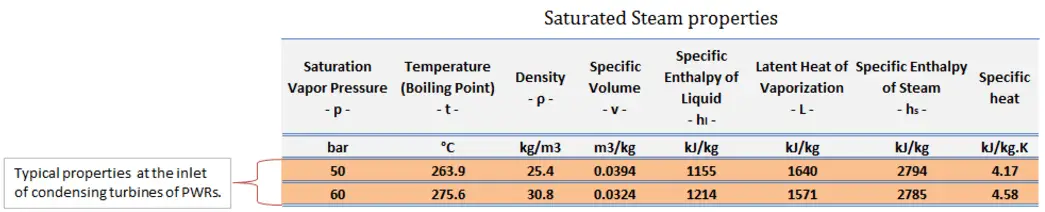
Typically most nuclear power plants operate multi-stage condensing steam turbines. The high-pressure stage receives steam (this steam is nearly saturated steam – x = 0.995 – point C at the figure; 6 MPa; 275.6°C). Since neither the steam generator is 100% efficient, there is always a temperature difference between the saturation temperature (secondary side) and the temperature of the primary coolant.
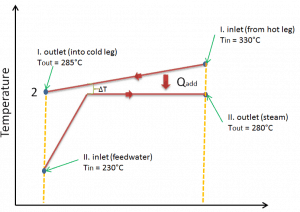
The hot primary coolant (330°C; 626°F) is pumped into the steam generator through the primary inlet in a typical pressurized water reactor. This requires maintaining very high pressures to keep the water in a liquid state. To prevent boiling of the primary coolant and provide a subcooling margin (the difference between the pressurizer temperature and the highest temperature in the reactor core), pressures around 16 MPa are typical for PWRs. The reactor pressure vessel is the key component, which limits the thermal efficiency of each nuclear power plant since the reactor vessel must withstand high pressures.