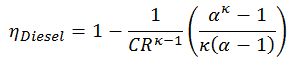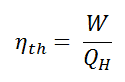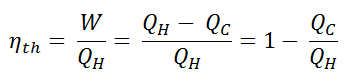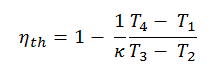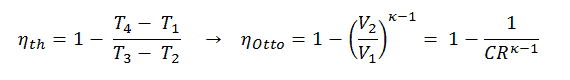Thermal efficiency for Diesel cycle:
where
- ηDiesel is the maximum thermal efficiency of a Diesel cycle
- α is the cut-off ratio V3/V2 (i.e., the ratio of volumes at the end and start of the combustion phase)
- CR is the compression ratio
- κ = cp/cv = 1.4
Thermal Efficiency for Diesel Cycle
Since Carnot’s principle states that no engine can be more efficient than a reversible engine (a Carnot heat engine) operating between the same high temperature and low-temperature reservoirs, the Diesel engine must have lower efficiency than the Carnot efficiency. A typical diesel automotive engine operates at around 30% to 35% of thermal efficiency. About 65-70% is rejected as waste heat without being converted into useful work, i.e., work delivered to wheels. In general, engines using the Diesel cycle are usually more efficient than engines using the Otto cycle. The diesel engine has the highest thermal efficiency of any practical combustion engine. Low-speed diesel engines (as used in ships) can have a thermal efficiency that exceeds 50%. The largest diesel engine in the world peaks at 51.7%.
In general, the thermal efficiency, ηth, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, QH.
The thermal efficiency, ηth, represents the fraction of heat, QH, converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:
The heat absorbed occurs during combustion of fuel-air mixture, when the spark occurs, roughly at constant volume. Since during an isochoric process there is no work done by or on the system, the first law of thermodynamics dictates ∆U = ∆Q. Therefore, the heat added and rejected is given by:
Qadd = mcp (T3 – T2)
Qout = mcv (T4 – T1)
Substituting these expressions for the heat added and rejected in the expression for thermal efficiency yields:
This equation can be rearranged to the form with the compression ratio and the cut-off ratio. Thermal efficiency for Diesel cycle:
where
- ηDiesel is the maximum thermal efficiency of a Diesel cycle
- α is the cut-off ratio V3/V2 (i.e., the ratio of volumes at the end and start of the combustion phase)
- CR is the compression ratio
- κ = cp/cv = 1.4
It is a very useful conclusion because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given fuel mass. As concluded in the previous section, the air-standard Otto cycle thermal efficiency is also a function of compression ratio and κ.
When we compare these to formulae, it can be seen that the Otto cycle will be more efficient for a given compression ratio (CR) than the Diesel cycle. But diesel engines are usually more efficient since they can operate at higher compression ratios.
In ordinary Otto engines, the compression ratio has its limits. The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1. Higher compression ratios will make gasoline engines subject to engine knocking, caused by the autoignition of an unburned mixture if lower octane-rated fuel is used. There is minimal risk of autoignition of the fuel because diesel engines are compression-ignition engines, and there is no fuel in the cylinder at the beginning of the compression stroke.
See also: Diesel Cycle – Problem with Solution.
See also: Compression Ratio