Facebook Instagram Youtube Twitter

Example of Isothermal Process

Isothermal process - pV diagram
Isothermal process – pV diagram

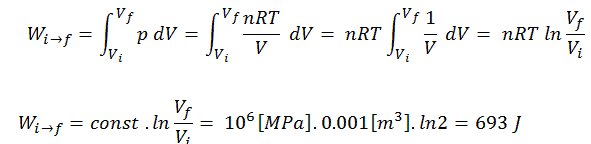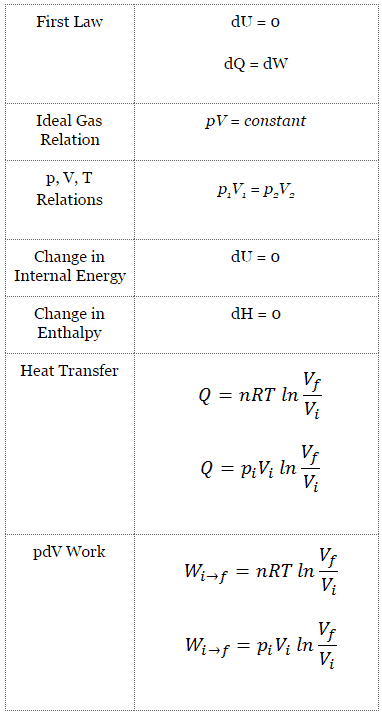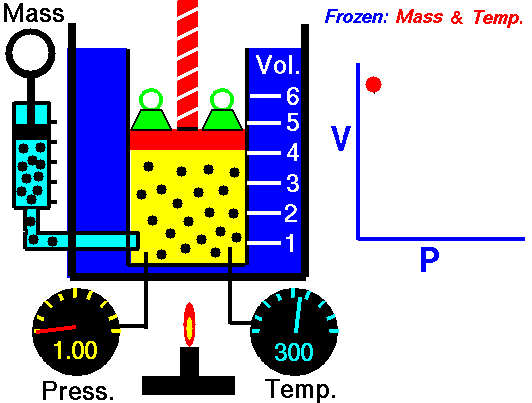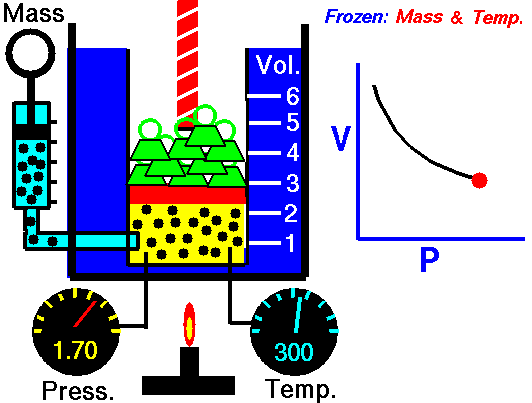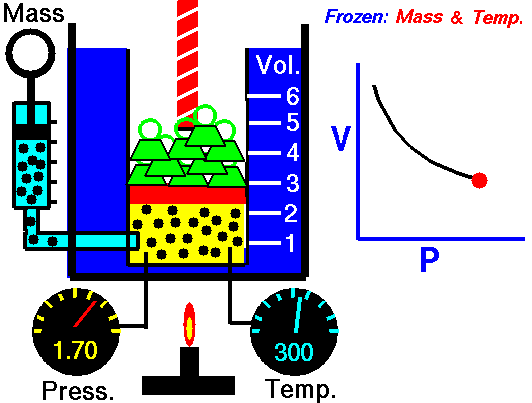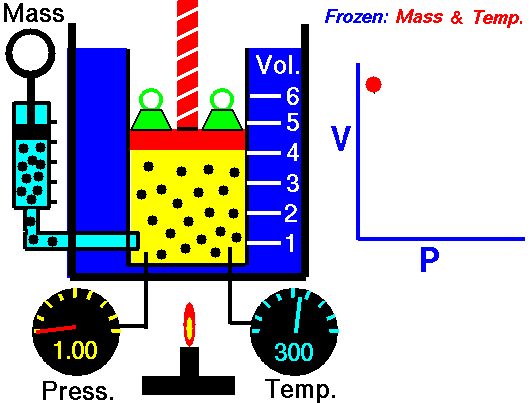
Assume an isothermal expansion of helium (i → f) in a frictionless piston (closed system). The gas expansion is propelled by the absorption of heat energy Qadd. The gas expands from an initial volume of 0.001 m3, and simultaneously the external load of the piston slowly and continuously decreases from 1 MPa to 0.5 MPa. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate the final volume of the chamber and then calculate the work done by the system when the temperature of the gas is equal to 400 K.

Solution:

The final volume of the gas, Vf, can be calculated using p, V, T Relation for isothermal process:

piVi = pfVf ⇒ Vf = piVi / pf = 2 x 0.001 m3 = 0.002 m3

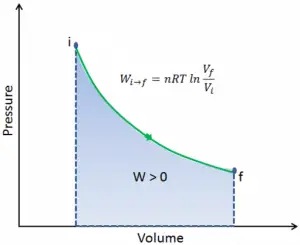
To calculate such processes, we would need to know how pressure varies with volume for the actual process by which the system changes from state i to state f. Since during this process the internal pressure was not constant, the p∆V work done by the piston must be calculated using the following integral:

isothermal process - example

By convention, a positive value for work indicates that the system in its surroundings does work. A negative value indicates that work is done on the system by its surroundings. The pΔV work is equal to the area under the process curve plotted on the pressure-volume diagram.

Isothermal process - main characteristics
Isothermal process – main characteristics
Boyle-Mariotte Law
Boyle-Mariotte Law. The volume is inversely proportional to the pressure for a fixed mass of gas at a constant temperature. Source: grc.nasa.gov NASA copyright policy states that “NASA material is not protected by copyright unless noted”.
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Isothermal Process